MayaNodeEditorを使ったアップベクター作成
Set UpVector using MayaNodeEditor

Maya内のデータは全てノードというのでそのノードが編集できるエディタをノードエディタと言います。
以下のMayaのドキュメントを覗くと、このような説明が書かれています。

■ドキュメント ノードエディタ（Node Editor）

アウトライナでディスプレイ内のDAGオブジェクトのみのチェックを外すと、
実はスタート時の新シーンでもたくさんのデータが既に存在していることが分かります。

ポリゴンの球を取り出すとノードエディタでは3つのノードが表示されます。
これらは、アトリビュートエディタでタブとして表示されているデータがノードとして表示されている、という状態です。

ノードは折りたたまれていて、展開するとより多くの接続ピンが表示されます。
pSphere1を展開すると、アトリビュートエディタ内の情報と同じく、移動/回転/スケールや可視性などが並んでいます。
これらのピンを線で繋げることによって動きが連動する、と分かります。

例えば円錐を取り出しその移動ピンに球の移動ピンをつなげれば、球を動かせば円錐も動くことが想像できます。

Maya2024ではノード作成ペインに数学という項目が追加され、計算に役立つノードが大幅に増えています。
右上の[ノード作成ペインの表示]を押すと取り出せるノードを見ることが出来ます。
またTABキーを押して、検索して、ノードを取り出すこともできます。

円周率（Pi）、累乗（Power）、正規化（Normalize）、正弦（Sin）など、まで無かったの？と思うような標準的な計算ノードから、間の角度（angleBetween）、長さ（length）、余弦（cos）、逆正弦（asin）などキャラクターリグ構築などに関わりがありそうなノードがそろっています。

ここでは、腕や脚の折曲がる方向を決めるものとします。
良く求められるデータとしては、3点（例えば、腕、肘、手の位置）が分かっている時、その3点で得られる平面（レゾリューションプレーン）上にある4点目をアップベクターの位置とします。

例えばIKで動く腕や脚の位置が分かっているモーションキャプチャーデータがある時に、アップベクターの位置を求めておくことで、キャラクターリグで動いているアニメーションを調整しやすいようにしておくことができます。

三角を求める関数から計算すれば良いので、色々な求め方があります。
また、DCCツールによって用意されている計算用のノードの違いや作りやすさによって設定方法を変えたりします。

まずは、Maya2024の標準ノードを使った方法を紹介します。
そして次にExprespyを利用してPythonによるアップベクターの求め方を紹介します。
あと参考として、MotionBuilderでの場合も軽く紹介しておきます。

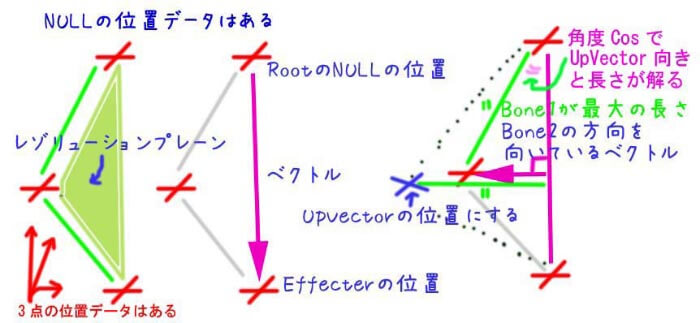
今回は、もっとも理解がしやすいのではないか？と思われる距離（Length）と方向（Vector）から求める考え方でノードを組んてみたいと思います。
全体像を先に見せてしまうと気が引ける…かも知れませんが、少しずつ組まれていく工程を説明しながら紹介します。

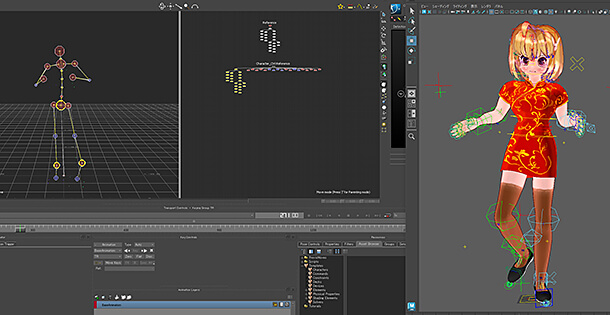
Rootが原点にあって、3つのジョイント、arm、elbow、wristはikHandleによって腕（又は脚）のように動く設定がしてあります。
wristとRootの中間地点にmid_posというロケータが見えるようにしてあります。
そして、その上にあたる肘の更に上に、今回求めるUpVectorが赤色のロケータで表示しています。
右側にある水色のロケータは、途中までの結果をテストして見れるように用意しているロケータです。

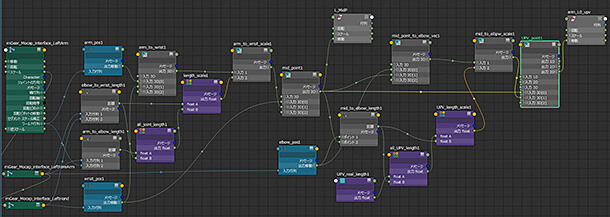
あらかじめ作成されたノードの状態を見てみます。
先ずは前半の黄色く囲った部分で、中間地点であるmid_posを求めています。
そして後半の黄色い枠内で、その中間地点を使ってUpVectorを求めています。
この２つの黄色い枠内は、全く同じノードの組み方をしています。
つまり、前半の黄色枠内が理解できれば、後ろも分かるということになります。
前後の黄色い枠内は何をしているかと言うと、距離と方向から位置を求めています。
この時、内積（Dot）/外積（Cross）やコサイン（Cos）などは使っていません。

先ずは前半、中間地点を求めてみましょう。

・距離（Length）＝間の距離（distanceBetween）
3つのジョイントの内、armとelbowの距離（長さ）を求めます。
そして同じくelbowとwristの距離（長さ）を求めます。
これには、左のペイン（項目欄）の数学から間の距離というノードを使用します。
これで2つのジョイント間の距離が解ったので、floatMathノードを使って2つの距離の合計値を得ます。
次に、elbowとwristの距離は、全体の距離の何割にあたるかを、同じくfloatMathノードを使って割り算をします。
途中まで得た結果を視覚的に見るには、水色で用意したテスト用のロケータを使うと便利ですが、値を見るにはfloatConstantノードを使うと小数点の付いた数値を確認することが出来ます。
先ほど割り算で得た値を見てみると、たまたまの数値ですが0.52となりました。これをスケール値として使用します。
（このスケール値はIKHandleを動かしても変化しませんが、骨自身の長さを変えたら、もちろん変化します）

・方向（Vector）＝減算（plusMinusAverage）
armとwristの位置から方向（ベクトル）を求めます。
これにはplusMinasAverageノードにそれぞのワールドの位置を使って引き算をして求めます。
そうしたら、先ほど計算したスケール値をmultiplyDivideノードを使って掛け算をします。
掛け算した結果を、テスト用の水色のロケータを使って確認してみます。
すると、原点から右に水色のロケータが位置しました。
本来求めているのはarmとewristの中間位置なのに、原点から始まった方向の位置になっているからです。
そこで、wristの位置を追加してあげれば良いことになります。
plusMinasAverageノードを使ってwristの位置を足し算してあげると、正しい中間地点mid_posが得ることが出来ます。

・アップベクターの位置 今紹介した方法の縦版 =同じ考え方
今度は、求めた中間位置mid_posからelbowの距離を求めておきます。
そして更に、elbowから2.0という追加の距離を足した値が全部の合計距離になります。
合計距離はfloatMathノードを追加にして求め、multiplyDivideノードをつかって除算（割り算）をします。
これで、前回と同じくスケール値が求められました。
前回と違うのは、中間位置からelbowの距離よりも、更に2.0長い距離になるので、約2倍近い、つまりスケール値は2.0に近い値になります。ここではたまたま1.7でした。
このスケール値を中間位置mid_posからelbowの方向（Vector）に掛け算をします。
この結果を、またテスト用の水色のロケータで見てみると、前回と同様に原点から始まった方向の位置になっています。
そこで正しいアップベクターの位置を求めるには、原点ではなく中間地点の位置を追加してあげれば良いことになります。
plusMinasAverageノードを使って中間地点の位置を足し算してあげると、正しいアップベクターの位置が得られることが出来ました。

Maya Exprespy（エクスプレスパイ）はGitHubで配信しているPythonによるエクスプレッション機能を提供するノードのプラグインです。
https://github.com/ryusas/maya_exprespy

Maya 2024 対応、Python3対応、サンプル多数

標準ノードでやった内容を踏まえて、今度はPythonで組んてみます。
Pythonで組む場合はOpenMayaを使って方向（MVector）計算をします。

こちらもノードエディタのノード群を始めて見た時と同じく、コードの長さに気が引けるかも知れませんが、
グローバルの位置を求めるのに使う記述などがいつものお決まりのパターン記述なので、計算式が大変な訳ではありません。

例えば、あるlocator1という名前のロケータのグローバル位置を求めるには、以下のように記載します。

nul_pos = api.MPoint(locator1.translate + locator1.rotatePivot + locator1.rotatePivotTranslate)
nul_pos *= locator1.parentMatrix

公開しているGuthubのplug-ins内を見ると、Maya2024に対応していることが分かります。
またドキュメントも日本語ですし、サンプルシーンも用意されています。ライセンスはMITライセンスです。

サンプルのシーンを見ると、コンストレイントの例などが用意されています。
Pythonの書かれ方は以下のようになっているので慣れておきましょう。

★ Python 複合代入演算子
+=  右辺の値と左辺の変数の値を足し算し変数に代入 
-=  右辺の値と左辺の変数の値を引き算し変数に代入 
*=  右辺の値と左辺の変数の値を掛け算し変数に代入
/=  右辺の値と左辺の変数の値を割り算し変数に代入
//= 右辺の値と左辺の変数の値を小数点以下切り捨てし変数に代入（整数除算代入）
%=  剰余代入
**= べき乗代入

MVector = MVector ^ MVector  外積
float = MVector * MVector　　内積

★ インポート済みモジュール
import sys
import math
import maya.api.OpenMaya as api
import maya.OpenMaya as api1
import maya.cmds as cmds
import maya.mel as mel

★ exprespy ノードの生成　（スクリプトエディタで）＜シェリフボタンに登録など＞
import exprespy
exprespy.create()

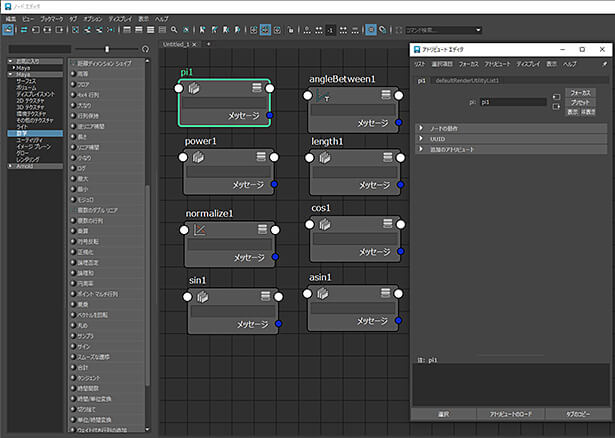
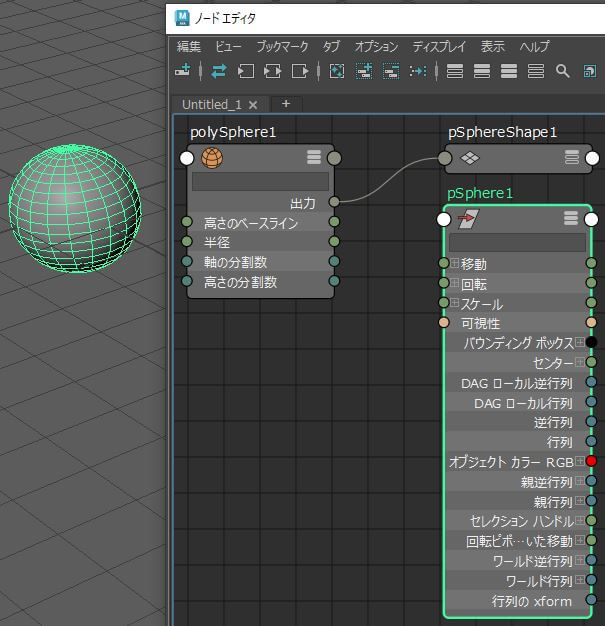
exprespyのノードをコマンドを使って生成してみると、ノードエディタにesprespy1というノードが作成されます。
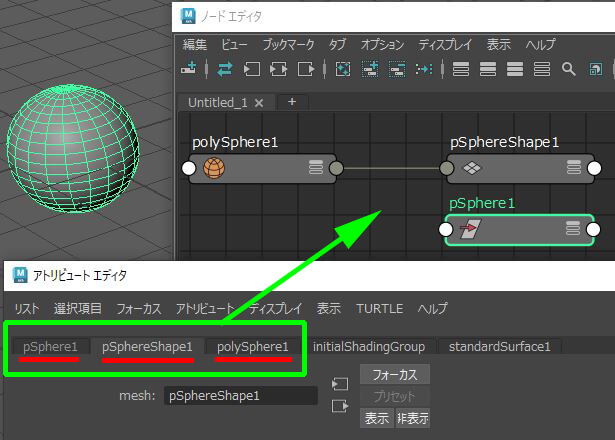
それを選択すると、アトリビュートエディタにコードが書ける欄Python Expression Codeが表示されます。
そこに上記ロケータ；locator1のグローバル位置を求める文字を記入した後ノードエディタを見ると、接続が完了しています。
この接続は手で繋げたのではなく、コードを記入すると自動的に繋がることが分かります。
サンプルシーンを見ると、方向コンストレイント、回転コンストレイント、アップコンストレイント、位置コンストレイントなど参考になるものが既に用意されています。

そして、ikHandleを動かすとアップベクターが動くという部分の解説です。
ノードエディタに表示されている3つのロケータArm、Elbow、Wristは階層構造になっていて、それぞれjoint_Arm、joint2_Elbow、joint3_Wristというジョイントの階層構造にペアレントコンストレイントが設定されていて、ジョイントの動きにロケータが追従して動くようにしてあります。
計算結果としてUpVectorというロケータ、Minus_UpVecorという折れ曲がる反対側に欲しい場合のアップベクター、そしてTEST１というテスト表示用の水色のロケータがあります。

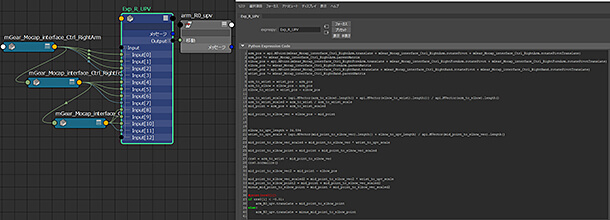
真ん中のUpVector_TESTというexprespyのノードを選択すると、アトリビュートエディタにコードが表示されます。
内容は前述のノードエディタの標準ノードで組み立てていた内容と同じことをしているだけです。
2点のグローバル位置から距離を、そしてスケール値を方向に掛け算をした位置に正しい起点を足し算で求めている事を2回しています。

ただし、肘からアップベクターの距離は、ここでは3.0としています。
また、途中で内積を使っている所は、ジョイントの階層構造がikHandleで引っ張られて一直線になった時、肘から3.0の距離の位置に留まって欲しい場合に、その下のif文内で使用しています。

以下にコードを記載しておきますので、参考にしてみてください。

elbow_to_upv_length = 3.0

arm_pos = api.MPoint(Arm.translate + Arm.rotatePivot + Arm.rotatePivotTranslate)
arm_pos *= Arm.parentMatrix
elbow_pos = api.MPoint(Elbow.translate + Elbow.rotatePivot + Elbow.rotatePivotTranslate)
upv_arm0 = api.MPoint(elbow_pos[0], elbow_pos[1], elbow_pos[2] + elbow_to_upv_length , 1)

elbow_pos *= Elbow.parentMatrix
upv_arm0_pos = upv_arm0 * Elbow.parentMatrix


wrist_pos = api.MPoint(Wrist.translate + Wrist.rotatePivot + Wrist.rotatePivotTranslate)
wrist_pos *= Wrist.parentMatrix

arm_to_wrist = wrist_pos - arm_pos
arm_to_elbow = elbow_pos - arm_pos
elbow_to_wrist = wrist_pos - elbow_pos

arm_to_wrist_scale = (api.MVector(arm_to_elbow).length() + api.MVector(elbow_to_wrist).length()) / api.MVector(arm_to_elbow).length()
arm_to_wrist_scaled = arm_to_wrist / arm_to_wrist_scale
mid_point = arm_pos + arm_to_wrist_scaled

mid_point_to_elbow_vec = elbow_pos - mid_point



wrist_to_upv_scale = (api.MVector(mid_point_to_elbow_vec).length() + elbow_to_upv_length) / api.MVector(mid_point_to_elbow_vec).length()
mid_point_to_elbow_vec_scaled = mid_point_to_elbow_vec * wrist_to_upv_scale
mid_point_to_elbow_point = mid_point + mid_point_to_elbow_vec_scaled

crs0 = arm_to_wrist ^ mid_point_to_elbow_vec

mid_point_to_elbow_vec2 = mid_point - elbow_pos

mid_point_to_elbow_vec_scaled2 = mid_point_to_elbow_vec2 * wrist_to_upv_scale
mid_point_to_elbow_point2 = mid_point + mid_point_to_elbow_vec_scaled2
minus_mid_point_to_elbow_point = mid_point + mid_point_to_elbow_vec_scaled2

print(crs0)
if crs0[1] < -0.01:
    UpVector.translate = mid_point_to_elbow_point
else:
    UpVector.translate = upv_arm0_pos

TEST1.translate = upv_arm0_pos
Minus_UpVector.translate = minus_mid_point_to_elbow_point

mGearで作ったコントロールリグにアップベクターのコントローラーがあります。
モーションキャプチャーから来たアニメーションをリグに乗せる際に、アップベクターの位置を計算してベイクする、というワークフローになります。

IK制御でキャラクターを動かしたい場合に、アップベクターの位置がアニメーションとして準備してあると、更なる動きの調整が必要な時にあらかじめ標準的な動きの位置が設定されていると修正しやすく便利だ、ということです。

このシーンはモーションキャプチャーのデータをキャラクターのリグに乗せるということを前提にしています。
従って、mGearのコントロールリグがMayaのHIKによって動いているシーンで説明しています。
左の腕用のアップベクターは、標準のノードエディタにあるノードで組んで求めた例、右腕はexprespyで求めた例にしてあります。
左右両方の腕のジョイントも、mGearのコントロールリグを動かしているHIK用のジョイントのグローバル位置から計算しています。そして左右とも求められた位置データをそれぞれarm_L0_upv_ctl、arm_R0_upv_ctlを位置コンストレイントしています。
アップベクターの位置を計算しなかった場合と比べると、mGear のアップベクターの位置はかなり異なっています。

この求められたアップベクターの位置は、動きに正解をもたらしているものではなく、あくまでもそれらしい位置を提供しているにすぎません。
最終的にはその動きに合わせて調整は必要なのですが、基準値があるとそこからの修正に便利だ、くらいに使うと良いと思います。

モーションキャプチャーデータを扱うMotionBuilderでもRelationalConstraintでアップベクターを求めることが出来ます。
用意されているノードや動作が異なる為、求め方も変えています。
MotionBuilderでアップベクターの位置を計算しておく利点は、モーションキャプチャーのデータをFBXで出力する段階でアップベクターの位置データがあれば、Mayaにインポートした時すぐに利用できる、といったところにあります。

今回はあくまでも紹介、としたいと思いますので、公開した動画は下に掲載しますが、気になる方は GTMF2013時の紹介ページを参照してみてください。

MotionBuilder2014 新機能 FlexibleMocapの使用例 その１Softimageとの連携 , UpVectorの計算

このようにして、アップベクターの位置を自動的に計算している仕組みを設定したMayaシーンを保存しておいて、
「Maya Pythonで作成するFBXモーションリターゲットツール」で中間ファイルとして利用しています。
そちらも参考にしてみてください。